1.2偏差与方差

1.2 偏差与方差

二者在深度学习上的现状

• 一般将二者分开考虑，并不考虑二者的权衡

偏差

• 偏差高，欠拟合
• 描述的是训练集的测试结果和事实标签之间的差距

方差

• 方差高，过拟合
• 描述的是训练集与验证集之间的准确性的差距

对比

• 高方差
  • Train set error: 1%
  • Dev set error: 11%
• 高偏差
  • Train set error： 15%
  • Dev ser error: 16%
• 高偏差,高方差
  • Train set error: 15%
  • Dev set error: 30%
• 低偏差，低方差
  • Train set error: 0.5%
  • Dev set error: 1%

最优误差

最优误差也被称为贝叶斯误差，是指在现有特征集上，任意可以基于特征输入进行随机输出的分类器所能达到的最小误差。比如说图片已经模糊到人眼无法分辨了，即使最优的分类器也无法分辨，此时最优误差便会大于零

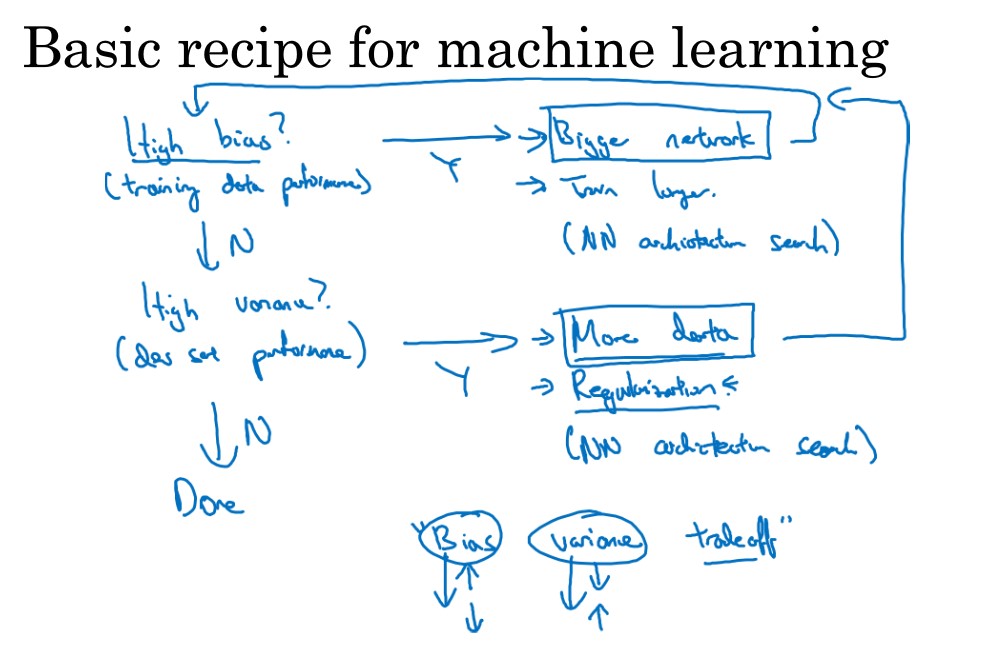
机器学习与方差和偏差的处理

模型训练流程

1. 初始模型训练
2. 首先知道偏差高不高
   1. 如果偏差比较高，试着评估训练集或训练数据的性能
   2. 如果偏差特别高，那么就要考虑选择一个新的网络了（
      • 更多隐藏层或隐藏单元的网络
      • 或者花更多的时间来训练网络
      • 或者尝试更先进的优化算法
3. 检查方差
   1. 如果方差比较高
      1. 最好的解决方法就是采用更多的数据
      2. 尝试通过正则话来减少过拟合
      3. 寻找更合适的神经网络架构

注意

• 必须要清楚的知道存在的问题使偏差还是方差，还是两者的问题
• 高偏差和高方差的解决方案是不同的
• 一般采用更大的网络和数据可以同时减小方差和偏差